Answer if one side of the triangle is 1/2 of the hypotenuse then the angle opposite to it is 30° and if the remaining side is √3/2 of the hypotenuse then the angle opposite to that side is 60° acobdarfq and 7 more users found this answer helpful heart outlined30°60°90° Right Triangles All 30°60°90° Right Triangles are formed by taking half of a Equilateral Triange, as shown in the steps below Because the original triangle is Equilateral, that means all three sides are the same length This is what variable "x" is trying to tell you All three sides are the same lengthNow take away the triangle on the right, leaving only the one on the left Now you have a 30°60°90° right triangle Use the Pythagorean theorem to calculate its altitude So the length of the altitude is Now memorize the way this right triangle looks and the lengths of the three sides
30 60 90 Triangles P4 Kate S Math Lessons
Pythagorean theorem 30 60 90 triangle
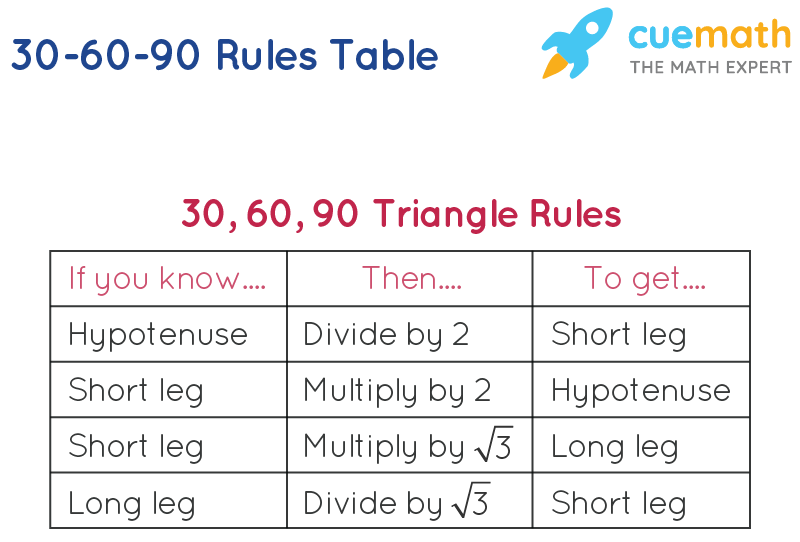
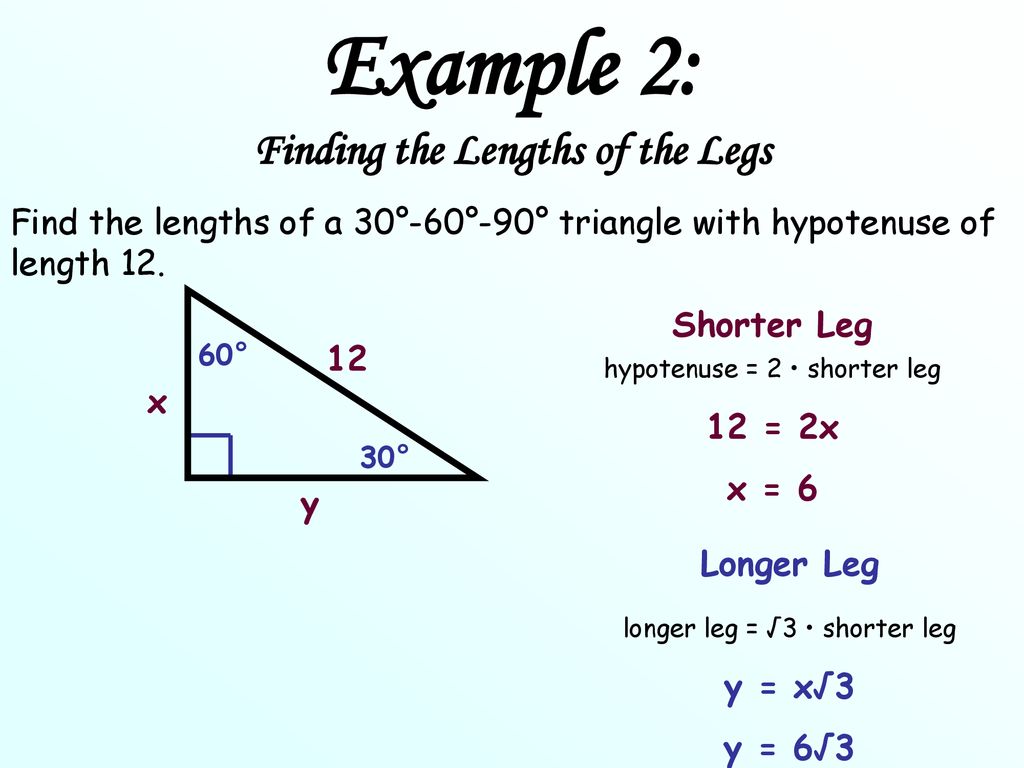
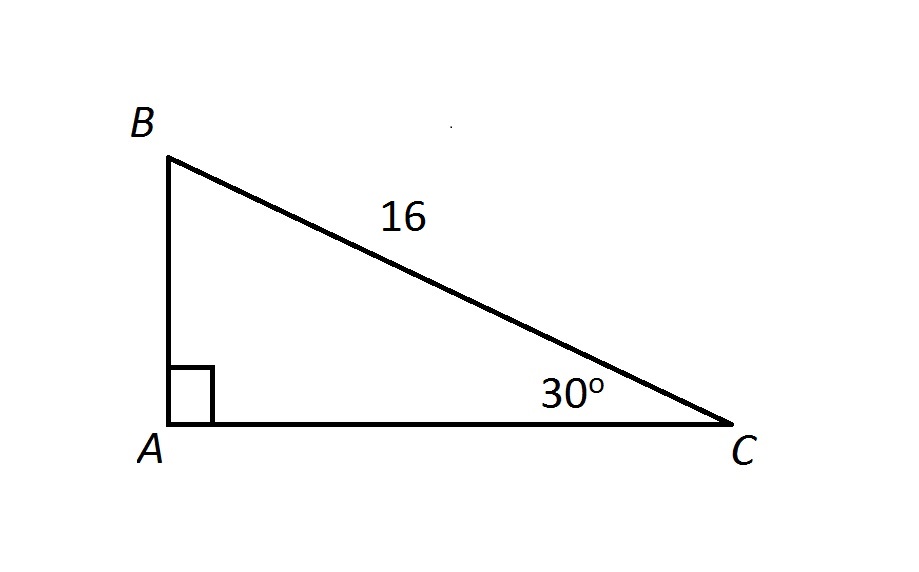
Pythagorean theorem 30 60 90 triangle-Theorem In a 30°60°90° triangle the sides are in the ratio1 2 We will prove that below (For the definition of measuring angles by "degrees," see Topic 12) Note that the smallest side, 1, is opposite the smallest angle, 30°;Given triangle is a 30˚60˚90˚ triangle Finding the value of a By 30˚60˚90˚ triangle theorem, Hypotenuse = 2 shorter length Here hypotenuse = 12, and shorter length = a 12 = 2 a a = 6 So, the value of a is 6 Finding the value of b By 30˚60˚90˚ triangle theorem, Longer length = √3 shorter length




30 60 90 Right Triangles Lesson Geometry Concepts Youtube
Honors Math Il Unit 5 Right Triangles Name Pyþhagorean Theorem Intro to Trig SOH CAH TOA Using trig to find the Missing Side Using Trig to Find the Missing Angle , Triangles Angles of Elevation and Depression and Word Problems pg 1 Points 10A 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of threeConcurrency of Medians of a Triangle 30°60°90° Triangle Theorem 45°45°90° Triangle Theorem Trigonometric Ratios Inverse Trigonometric Ratios Area of a Triangle Polygons and Circles Polygon Exterior Angle Sum Theorem Polygon Interior Angle Sum Theorem Regular Polygon Properties of Parallelograms Rectangle
Special Right Triangles Although all right triangles have special features – trigonometric functions and the Pythagorean theorem The most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 trianglesOf all these special right triangles, the two encountered most often are the 30 60 90 and the 45 45 90 triangles For example, a speed square used by carpenters is a 45 45 90 triangle In the day before computers when people actually had to draw angles, special tools called drawing triangles were used and the two most popular were the 30 60 90In a triangle, the ratio of the sides is always in the ratio of 1√3 2 This is also known as the triangle formula for sides yy√32y Let us learn the derivation of this ratio in the triangle proof section Consider some of the examples of a degree triangle with these side lengths
The triangle is a special right triangle, as it has a special relationship between its sides If we know the measure of at least one side of the triangle, the special proportions of sides of the triangle could be used to determine the measure of other sides of the same triangle Answer A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherIn mathematics, the triangle theorem states the ratio of the shortest side (opposite to angle 30∘ 30 ∘ ), to the longer side (opposite to angle 60∘ 60 ∘ ), and to the hypotenuse




Special Right Triangles Review Article Khan Academy
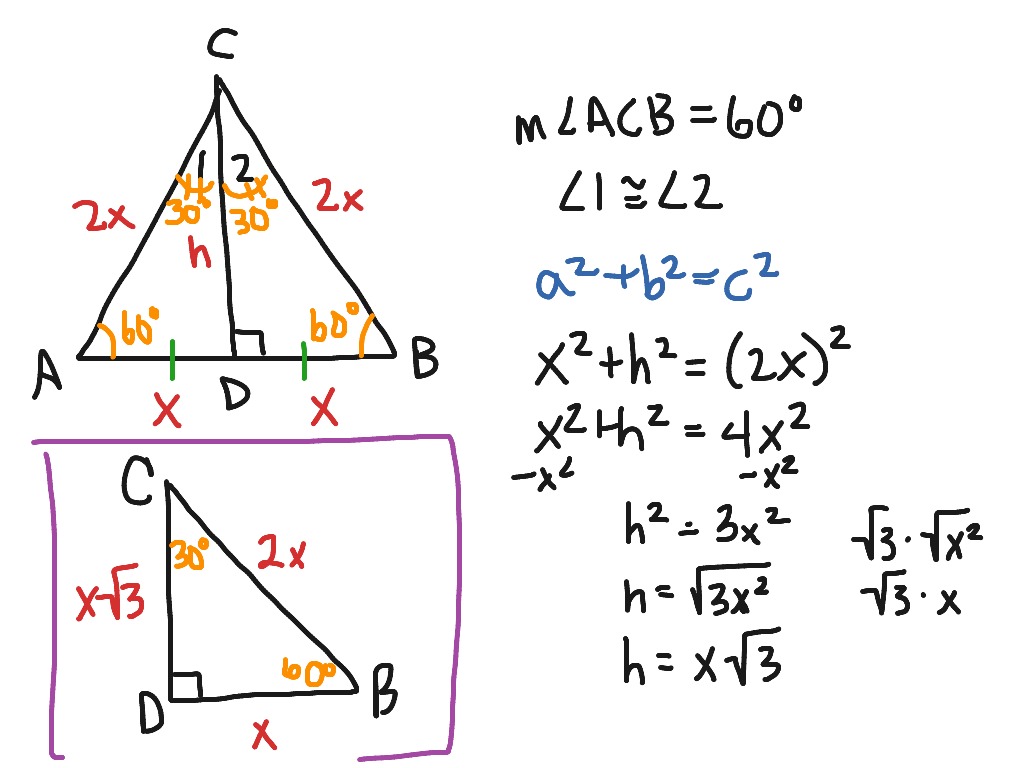



30 60 90 Triangle Math Right Triangles Showme
tan (60) = √3/1 = 173 The right triangle is special because it is the only right triangle whose angles are a progression of integer multiples of a single angle If angle A is 30 degrees, the angle B = 2A (60 degrees) and angle C = 3A (90 degrees) Thanks to this 30 60 90 triangle calculator you find out that shorter leg is 635 in because a = b√3/3 = 11in * √3/3 ~ 635 in hypotenuse is equal to 127 in because c = 2b√3/3 = 2a ~ 127 in area is 349 in² it's the result of multiplying the legs length and dividing byTheorem Application of Pythagoras #short #shortvideo #shortsfeed



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




Solved 1 For A 30 60 90 Triangle It Is Known That The Chegg Com
Geometry Theorem 87 ( triangles) multiply by 2 multiply by the square root of 3 divide by 2 divide by 2 to get the short leg, then If you are given the short leg and you are trying to find the If you are given the short leg and you are trying to find the If you add 30 to 90 you get 1 180 minus 1 leaves you with 60 degrees for that third angle Now that we know it's a 30 60 90 triangle, we can apply our 30 60 90 rules to finding the length of our ramp Our ramp is across from the 90View Notes 30 60 90 triangle theorem from MATH Mathematic at Roseville High School Lesson55notebook October31,14 Studentswillbeableto Date31Oct14 Lesson 55 #1 Prove and use the 30 60 90



1




30 60 90 Triangle Theorem Ratio Formula Video
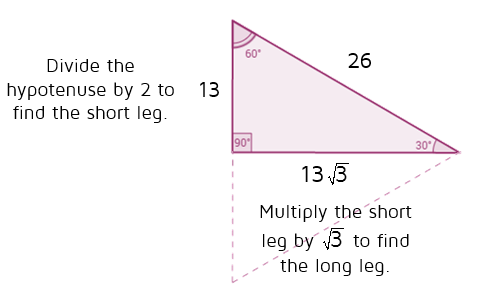
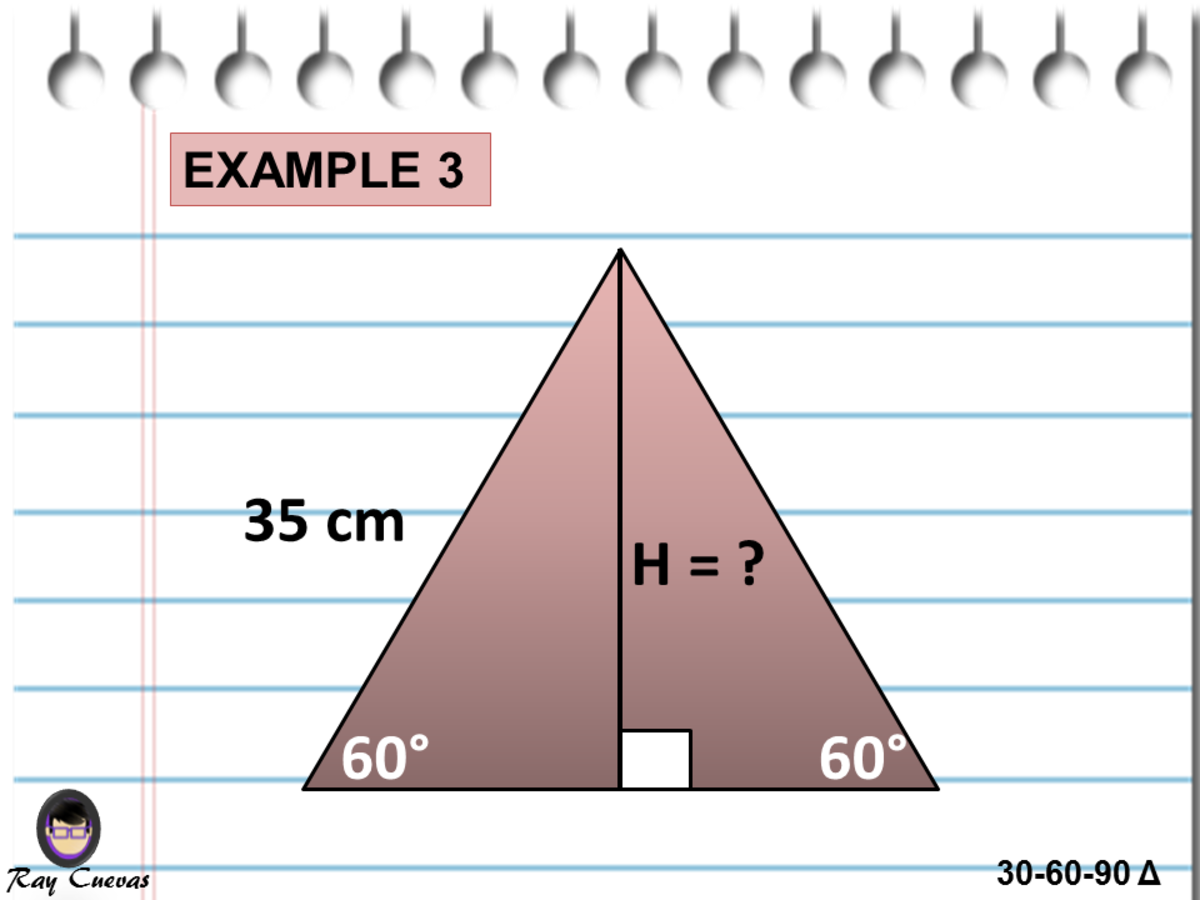
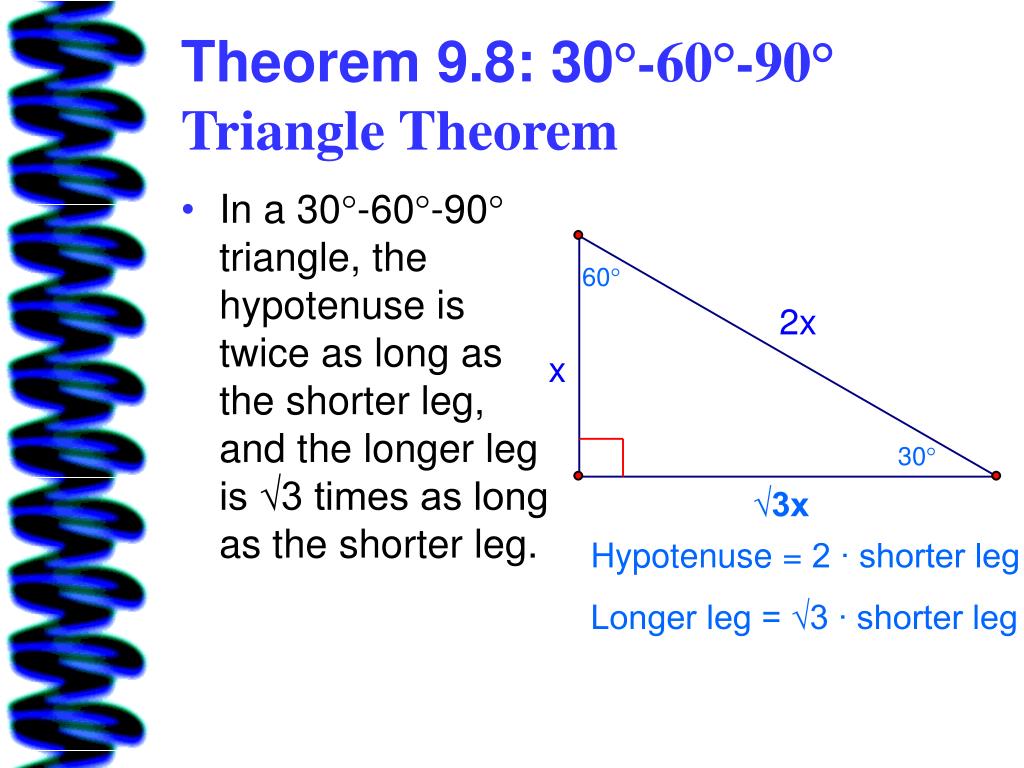
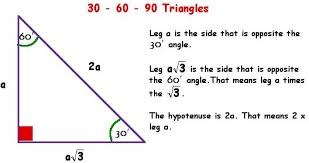
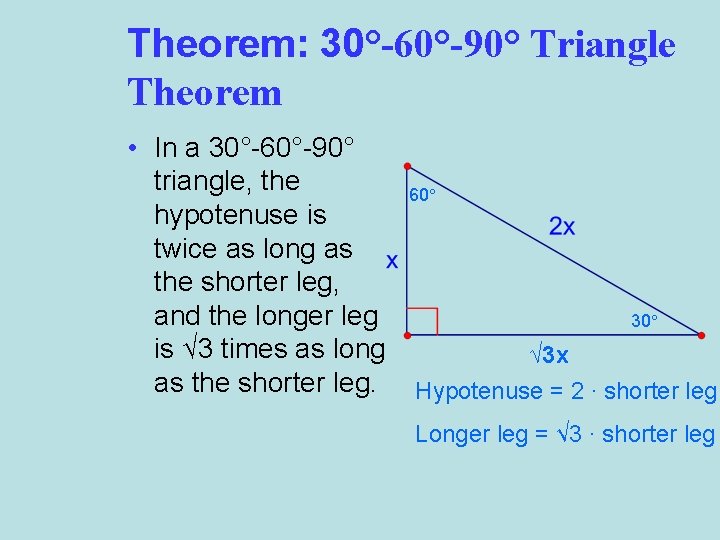
The 30°–60°–90° Triangle Theorem states "the length of the hypotenuse in a 30°–60°–90° triangle is two times the length of the shorter leg, and the length of the longer leg is √ __ 3 times the length of the shorter leg" 8 Use the Pythagorean Theorem to demonstrate the 30°–60°–90° Triangle Theorem The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of the SAT Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another The basic triangle ratio is Side opposite the 30° angle x Side opposite the 60° angle x * √ 3 Side opposite the 90° angle 2 x




Special Right Triangles Gmatsyllabus Com




30 60 90 Triangle Theorem Ratio Formula Video
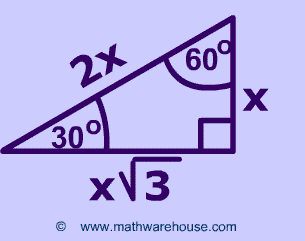
To find the longer leg, or a, you can simply multiply it by the square root of 3 to get 8 square root 3 To find the hypotenuse, or b, you can simply multiply by the shorter leg by 2 Thus, it will be 8 * 2 = 16 Here is a triangle with one side length givenWhile the largest side, 2, is opposite the largest angle,Triangle theorem To solve for the hypotenuse length of a triangle, you can use the theorem, which says the length of the hypotenuse of a triangle is the 2 times the length of a leg triangle formula



Mrwadeturner 30 60 90 Triangle 6th



Solve A 30 60 90 Triangle With Gradea
A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherTriangle in trigonometry In the study of trigonometry, the triangle is considered a special triangleKnowing the ratio of the sides of a triangle allows us to find the exact values of the three trigonometric functions sine, cosine, and tangent for the angles 30° and 60° For example, sin(30°), read as the sine of 30 degrees, is the ratio of the sideIn this video you can learn theorem of 30°60°90° triangle with the help of figure#trianglesstd9th#trianglesclass9#triangletheoremproof#30°60°90°tri




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




How To Work With 30 60 90 Degree Triangles Education Is Around
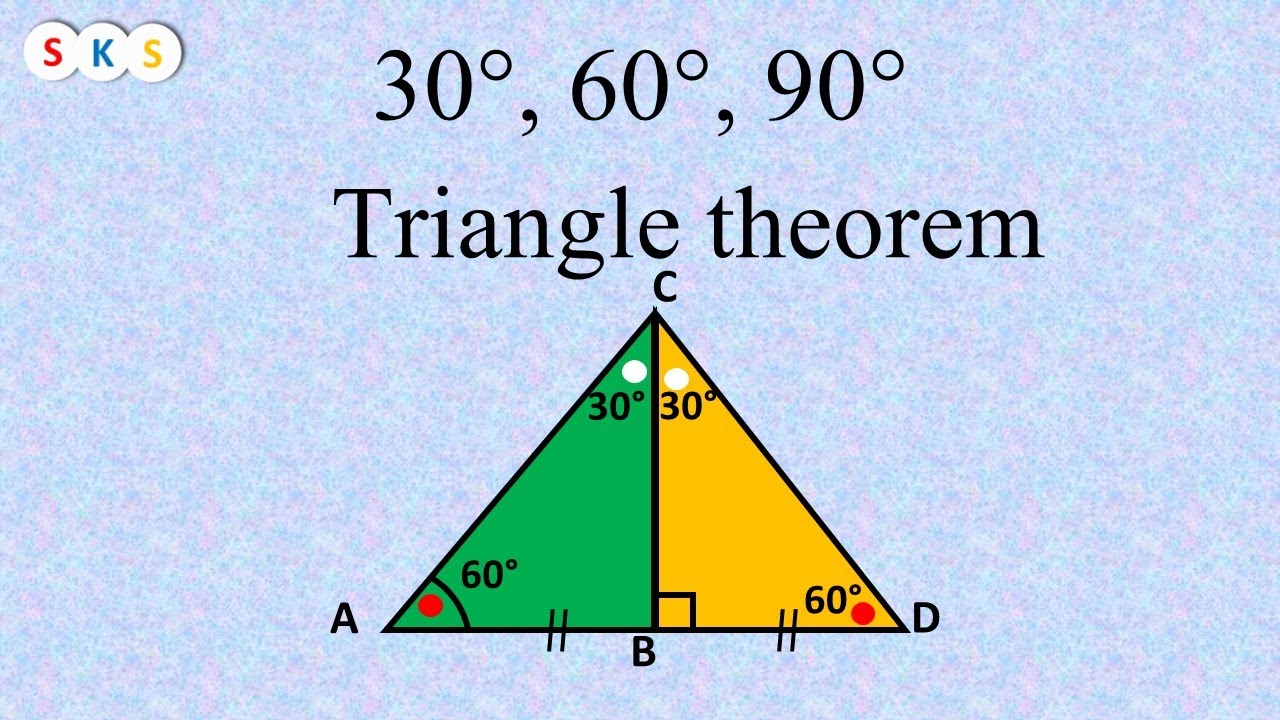
The Pythagorean Theorem can again be used to prove the Triangle Theorem Given Triangle ABC is a triangle Prove c=2a, Draw triangle ADC so that triangle ABC is congruent to triangle ADC When two triangles are congruent, their angles are equal So, m Triangles An equilateral triangle is a triangle with all sides congruent From the Isosceles Triangle Theorem if follows that the angles of an equilateral triangle are all the same Since the angles of any triangle add to 180 o, each angle of an equilateral triangle must be 60 o When an equilateral triangle is cut in half, you getThe triangle is also a right triangle The Formulas of the Given that X is the shortest side measure, we know we can measure out at the baseline for length X , turn an angle of 60 degrees, and have a new line that eventually intersects the line from the larger side at exactly 30



45 45 90 Special Right Triangle Calculator Inch Calculator
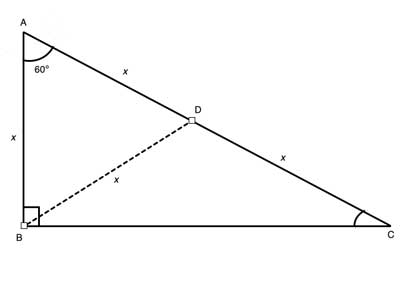



30 60 90 Triangle Geometry Help
30°60°90° Triangle Theorem In a 30°60°90° triangle, the hypotenuse is twice as long as the shorter leg, and the longer leg is √3 times as long as the shorter leg side opposite 30° is x, side opposite 60° x√3 and side opposite 90° is 2xAs one angle is 90, so this triangle is always a right triangle As explained above that it is a special triangle so it has special values of lengths and angles The basic triangle sides ratio is The side opposite the 30° angle x The side oppositeThe 30°–60°–90° triangle is the only right triangle whose angles are in an arithmetic progression The proof of this fact is simple and follows on from the fact that if α, α δ, α 2δ are the angles in the progression then the sum of the angles 3α 3δ =
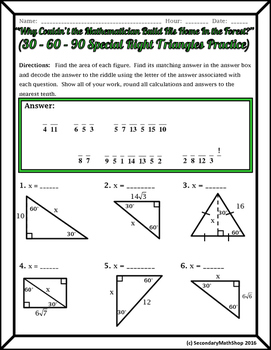



Right Triangles Special 30 60 90 Riddle Practice Worksheet Tpt
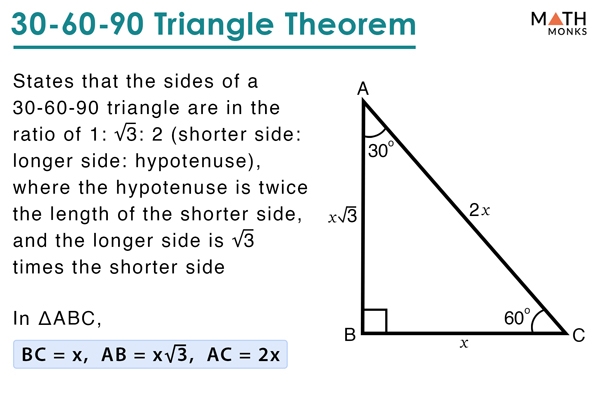



30 60 90 Triangle Definition Formulas Examples
The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x Long side (opposite the 60 60 degree angle) = x√3 x 3Answer (1 of 3) A triangle is special because of the relationship of its sides Hopefully, you remember that the hypotenuse in a right triangle is the longest side, which is also directly across from the 90 degree angle It turns out that in a triangle




30 60 90 Right Triangles Ck 12 Foundation
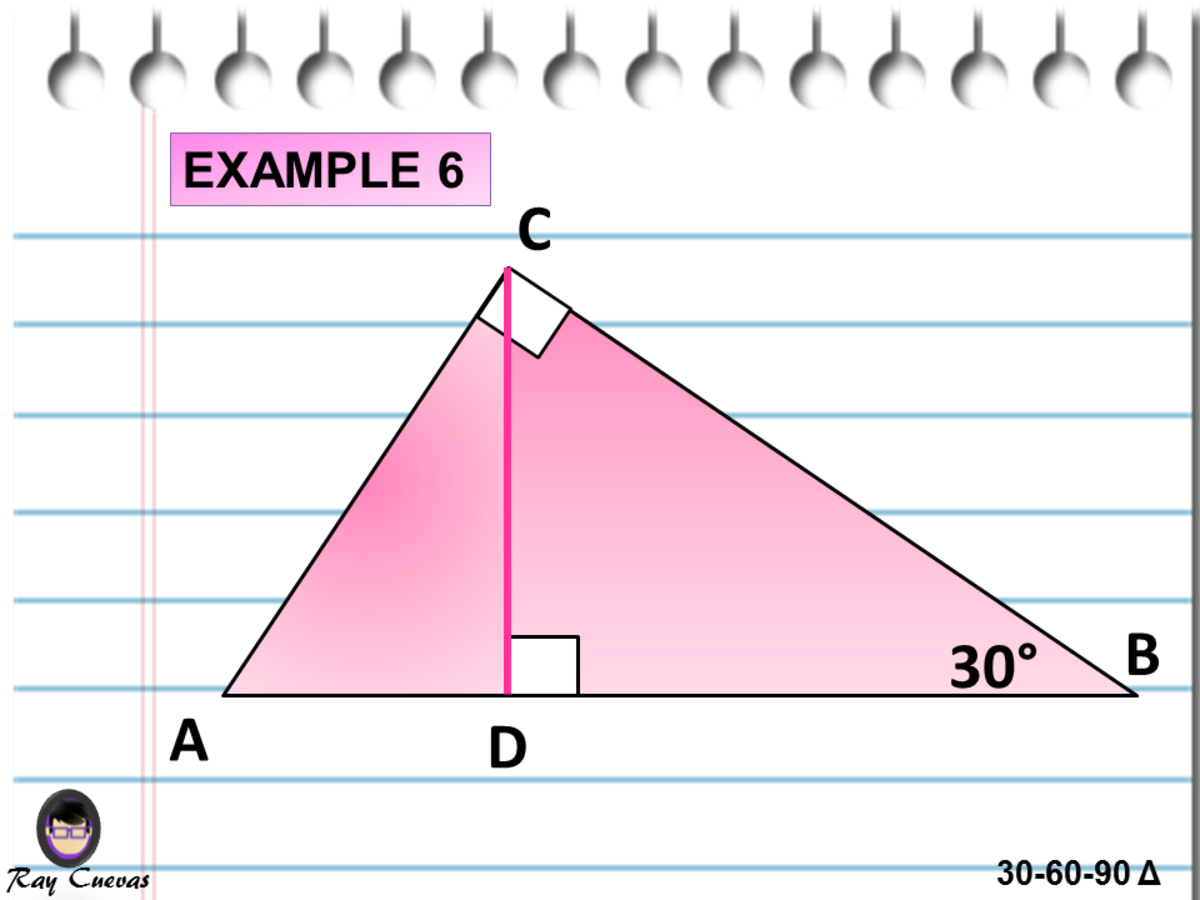



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Ratio Formula Video




Special Right Triangles Video Lessons Examples And Solutions




Foundation Class X Theorem Of 30 60 90 Triangle In Marathi Offered By Unacademy



Special Right Triangles Proof




30 60 90 Triangle Theorem Ratio Formula Video



Special Right Triangle 30 60 45 45 37 53 Elearning



Special Right Triangles 45 45 90 And 30 60 90 Geometry Foldable Tpt
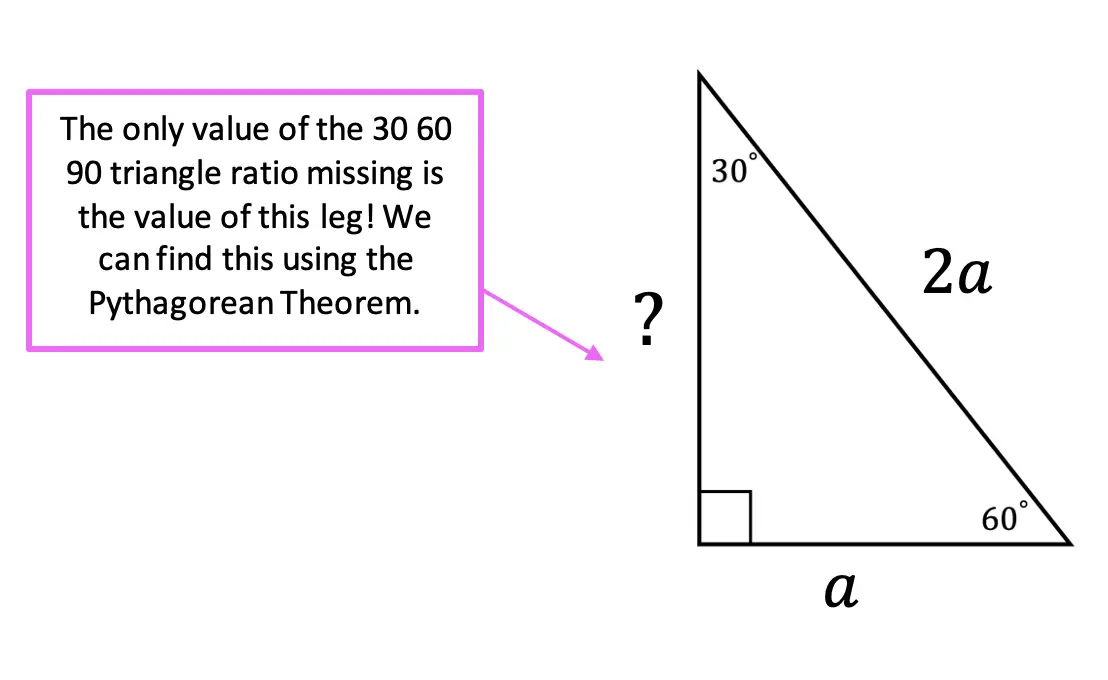



30 60 90 Special Triangles Geometry Mathsux 2



1
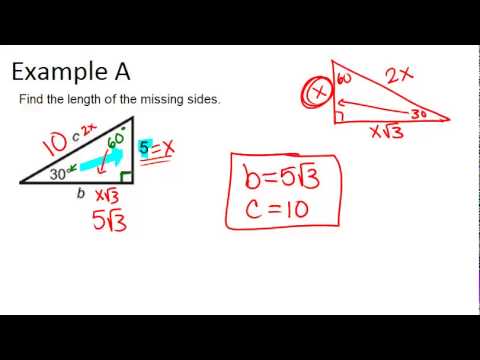



30 60 90 Right Triangles Examples Geometry Concepts Youtube




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
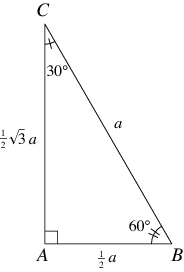



30 60 90 Triangle From Wolfram Mathworld




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com
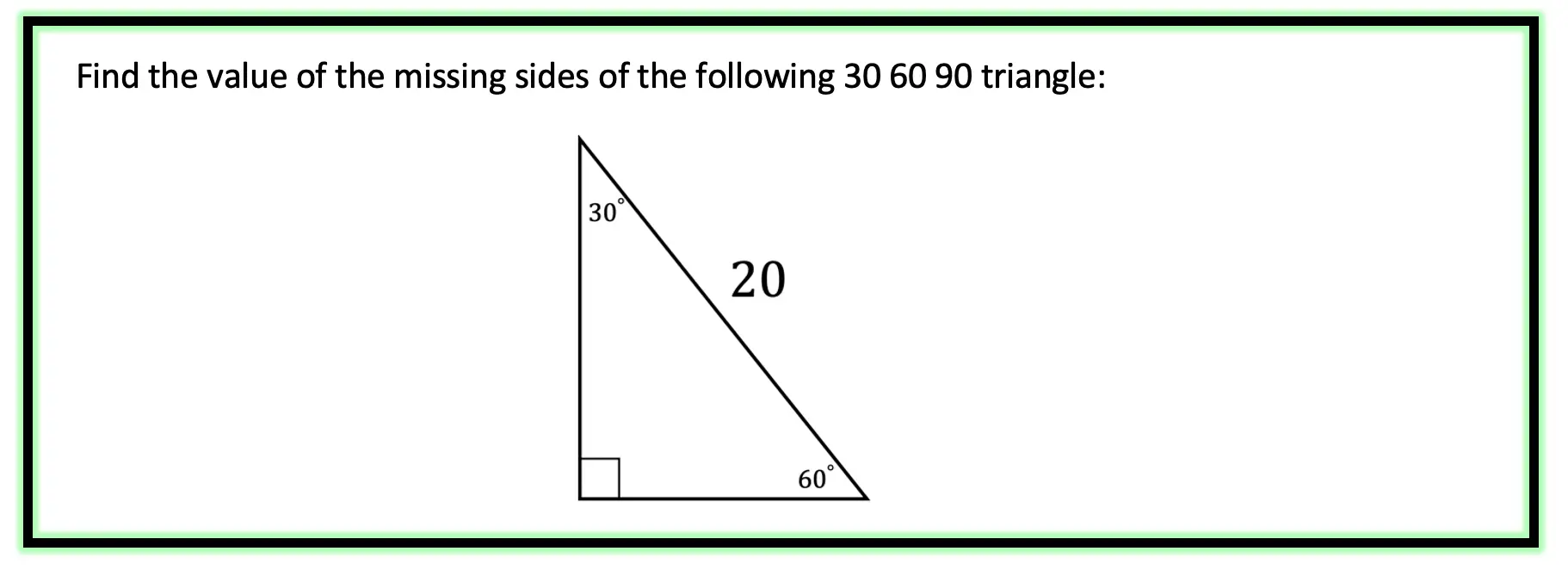



30 60 90 Special Triangles Geometry Mathsux 2




30 60 90 Right Triangles Solutions Examples Videos
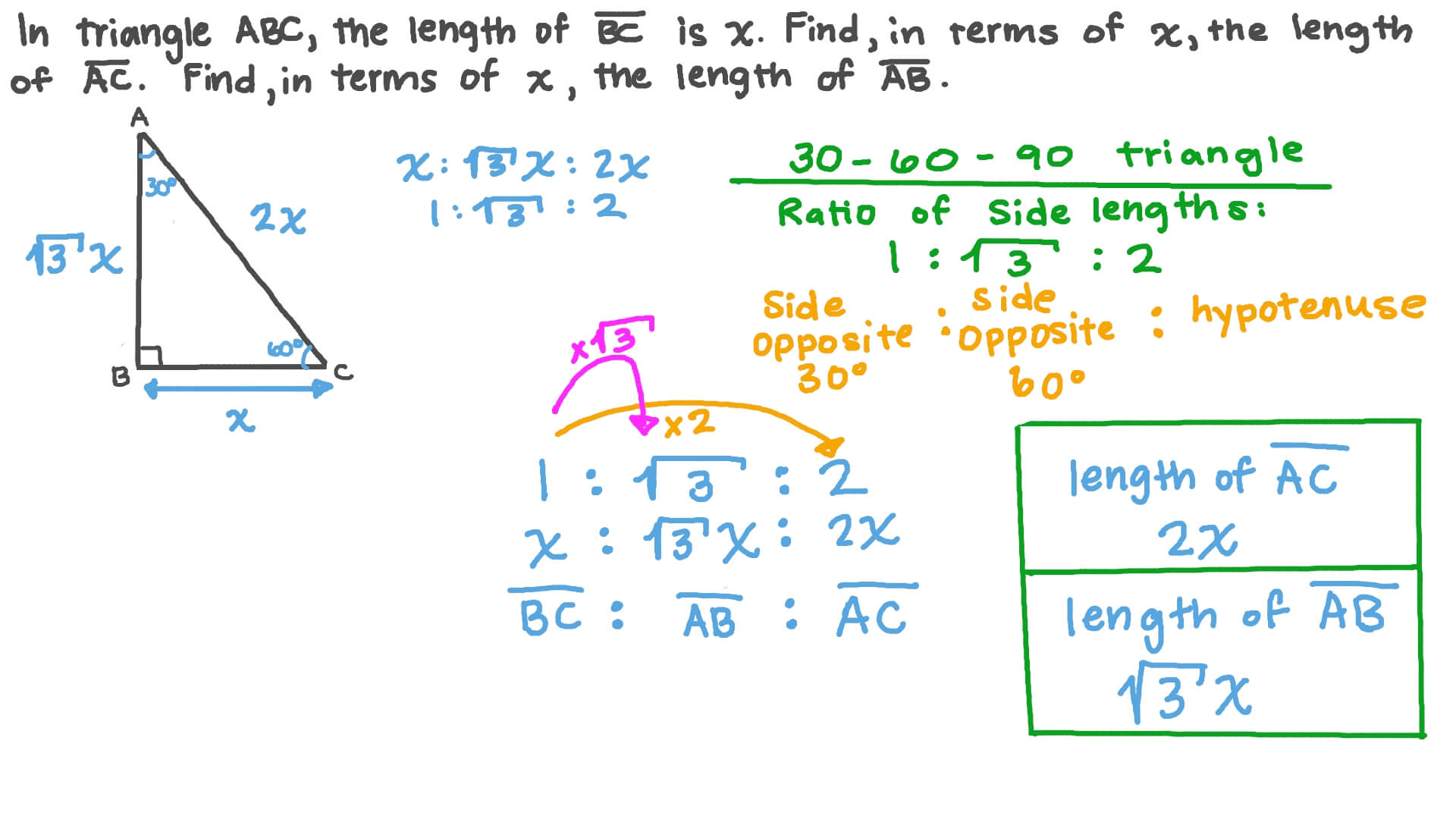



Question Video The Side Lengths Of 30 60 90 Triangles Nagwa




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
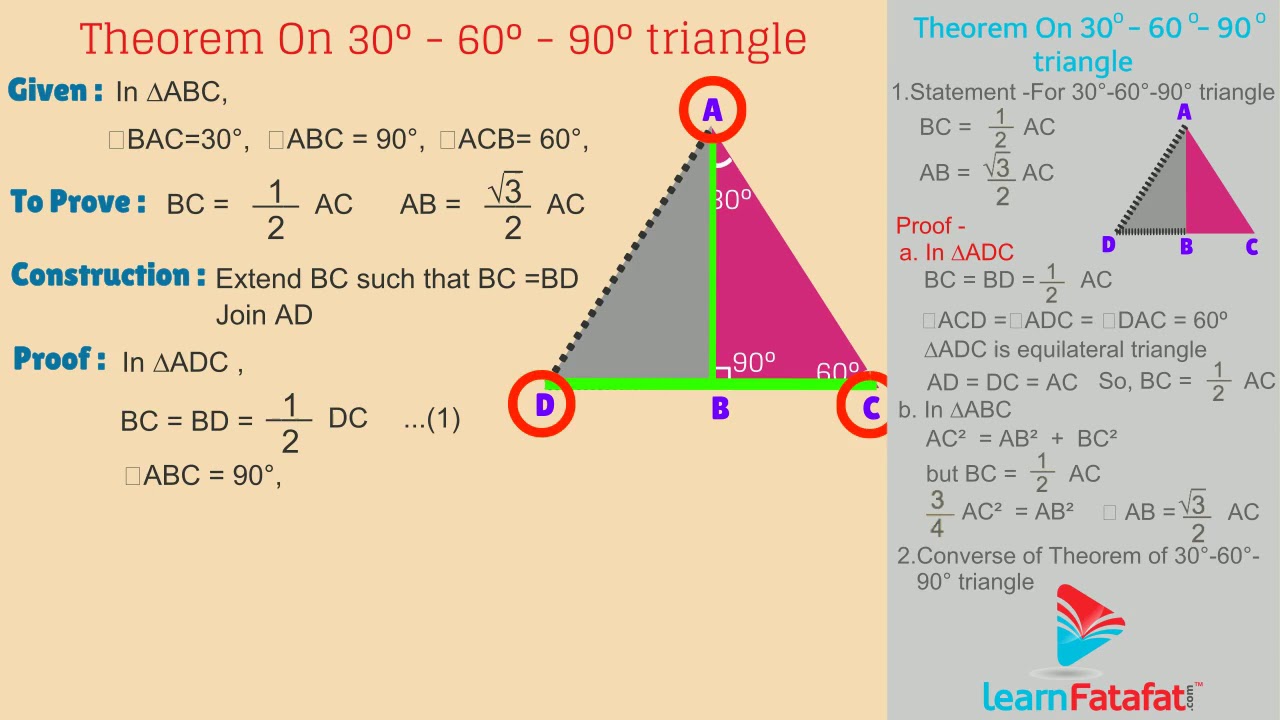



Pythagoras Theorem On 30 60 90 Triangle Youtube




30 60 90 Triangles P4 Kate S Math Lessons




30 60 90 Triangles
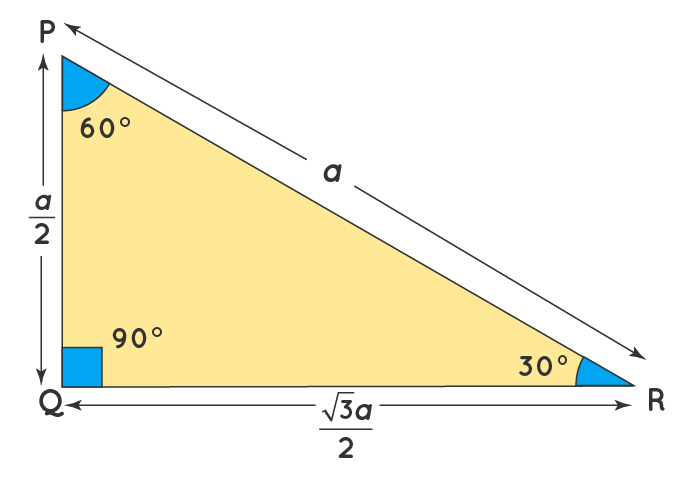



30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Theorem Ratio Formula Video



Ppt 9 4 Special Right Triangles Powerpoint Presentation Free Download Id
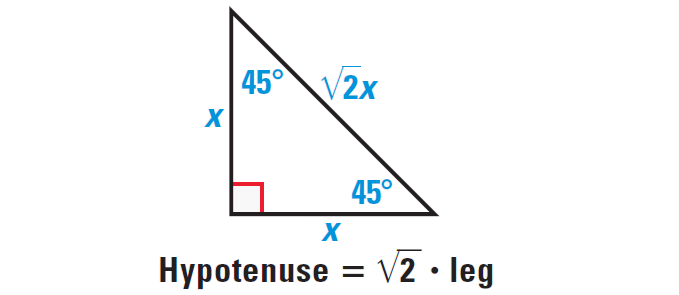



Theorems About Special Right Triangles




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




What Is A 30 60 90 Degree Triangle Virtual Nerd Can Help




30 60 90 Triangle Theorem Proof Don T Memorise Youtube




30 60 90 Triangle Calculator Formula Rules



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures




30 60 90 Triangle Calculator Formula Rules



1



Objective To Use The Properties Of 30 60 90 Triangle Ppt Download
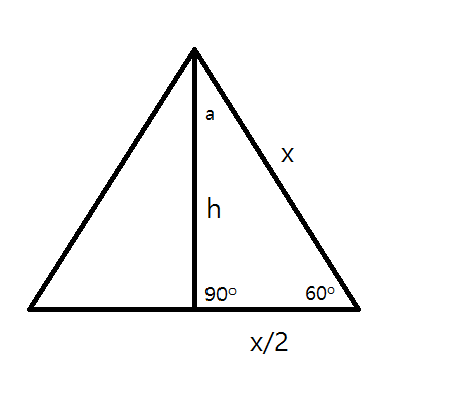



What Is A 30 60 90 Triangle Please Give An Example Socratic




30 60 90 Triangle Formulas Rules And Sides Science Trends




In Abc By 30 60 90 Triangle Theorem Brainly In



Why In A 30 60 90 Triangle Is The The Side Opposite 60 Degrees X Sqrt 3 Quora




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
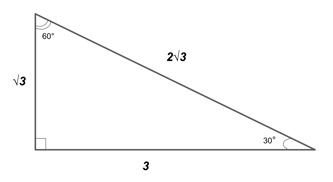



The Easy Guide To The 30 60 90 Triangle
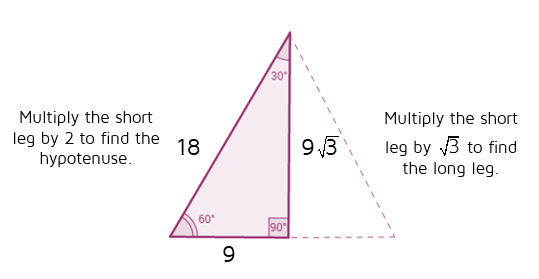



30 60 90 Triangles P4 Kate S Math Lessons




30 60 90 Right Triangle Side Ratios Expii




30 60 90 Right Triangles Lesson Geometry Concepts Youtube




5 30 60 90 Triangles Geometry15a




Ppt 30 60 90 Right Triangles Powerpoint Presentation Free Download Id
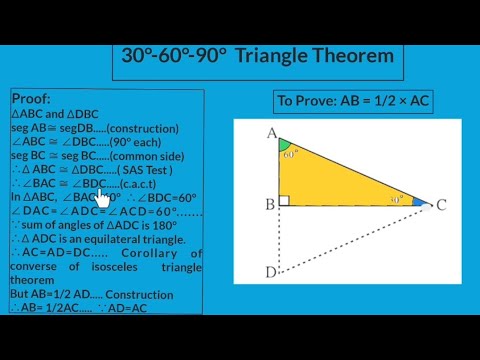



9th Maths 2 30 60 90 Triangle Theorem Youtube




30 60 90 Triangles Special Right Triangle Trigonometry Youtube



30 60 90 Right Triangle Theorem By Stephanie Joaquin Infographic



30 60 90 Triangle



30 60 90 Triangle Theorem Proof I Triangle I Theorem Of 30 60 90 Triangle Proof Youtube




30 60 90 Triangles



Special Triangles Hiset Math




30 60 90 Special Right Triangle Calculator Inch Calculator




A Quick Guide To The 30 60 90 Degree Triangle Dummies



5 5 Special Triangles
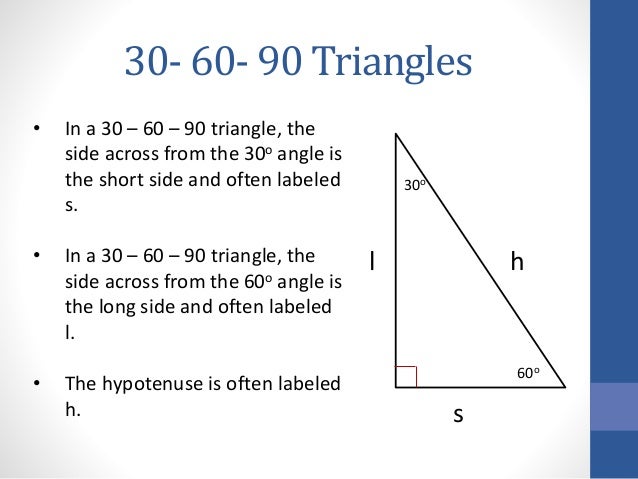



30 60 90 Triangles




30 60 90 Triangle Definition Theorem Formula Examples




The Complete Guide To The 30 60 90 Triangle



1



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangles Hd Youtube
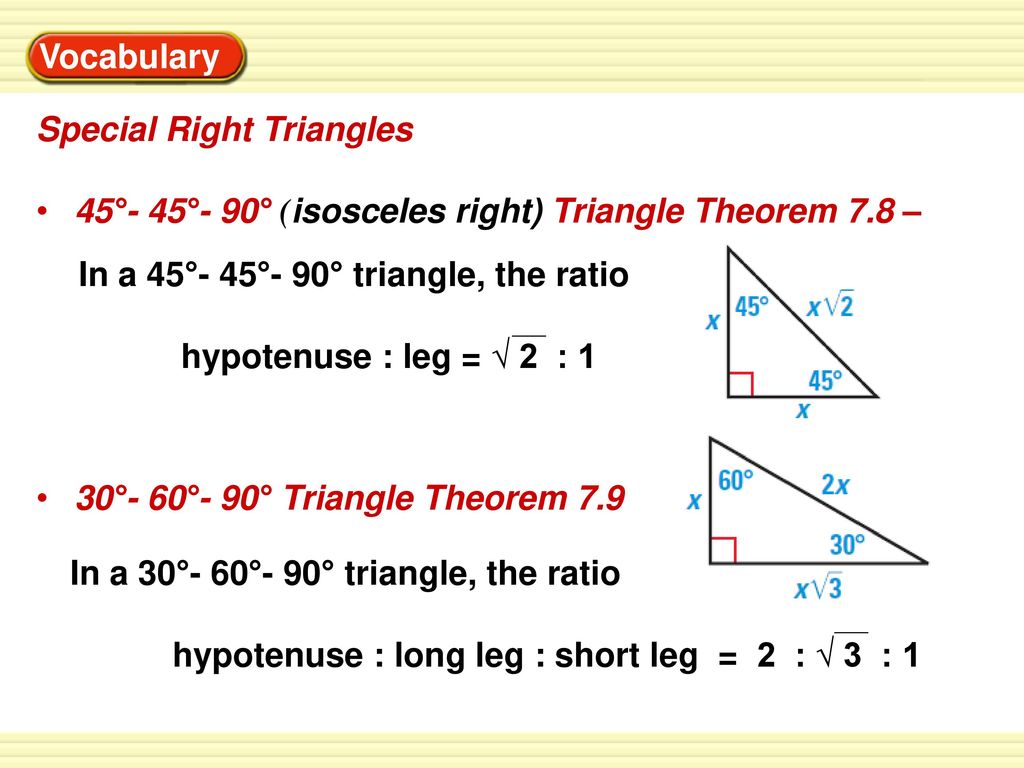



Simplify Answer Answer 12 Answer Ppt Download



45 45 90 And 30 60 90 Triangles Zona Land Education



Mrwadeturner 30 60 90 Triangle 6th
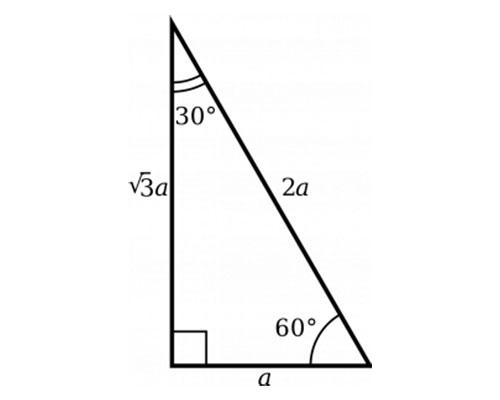



30 60 90 Triangle Sides Examples Angles Full Lesson




30 60 90 Triangle Definition Theorem Formula Examples




The Complete Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Ratio Formula Video




Learn About The 30 60 90 Triangle Caddell Prep Online




Chapter 8 Right Triangles Trigonometry 8 2 Special Right Triangles Ppt Download




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies




Special Right Triangles Fully Explained W 19 Examples




A Quick Guide To The 30 60 90 Degree Triangle Dummies



Special Right Triangles Proof
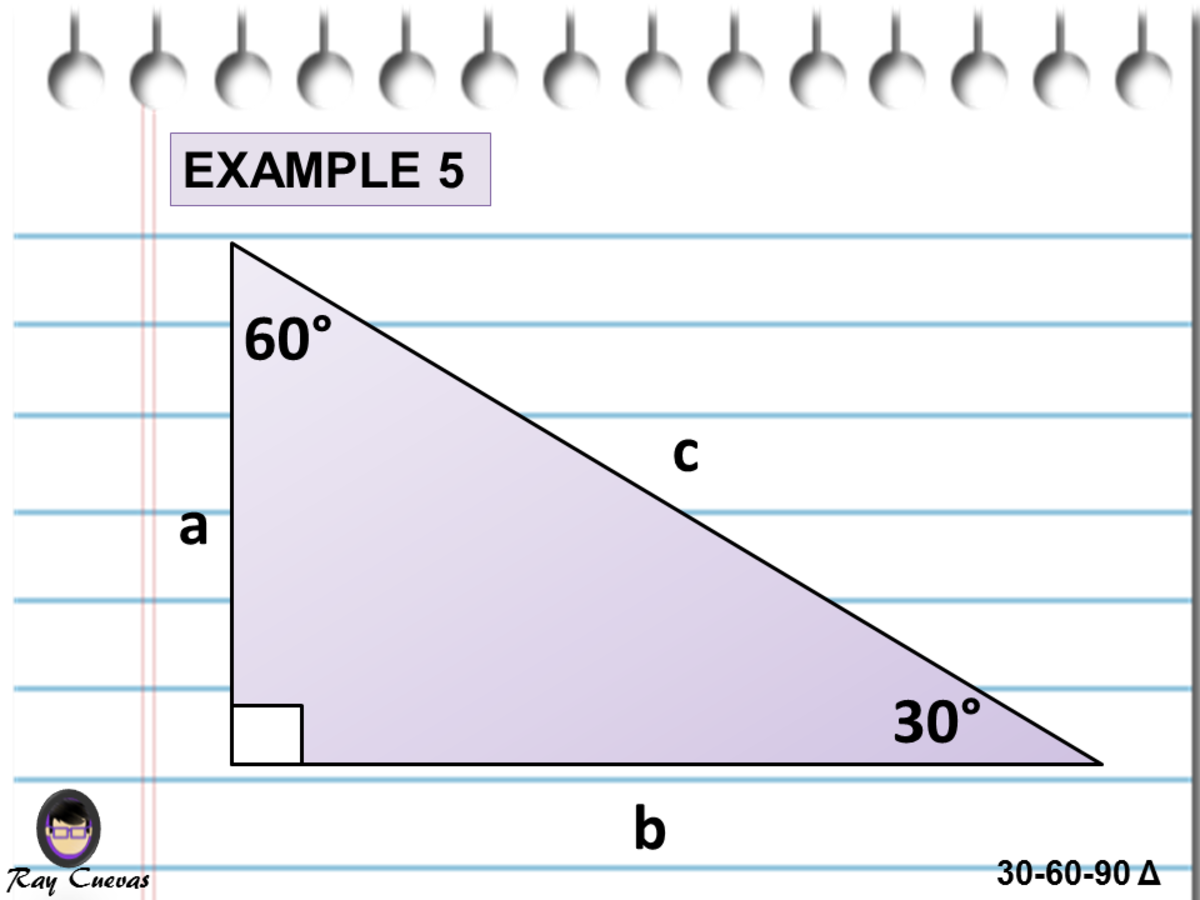



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



5 5 Special Triangles




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Right Triangles Read Geometry Ck 12 Foundation



Special Right Triangles Theorem 4590 Triangle Theorem In



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems



30 60 90 Triangles




30 60 90 Triangle Explanation Examples




30 60 90 Right Triangles Read Geometry Ck 12 Foundation




30 60 90 Right Triangles Read Geometry Ck 12 Foundation



0 件のコメント:
コメントを投稿